Fig. 1
Internal Ballistics of Muzzleloaders
This chapter is about how the chemical energy stored in the powder charge is converted into the kinetic energy of
the projectile (muzzle energy) and how the efficiency of this process is influenced by powder weight, powder granulation
(burning rate), caliber, barrel length, and projectile weight.
Like any firearm, a muzzleloader can be considered as a piston engine with internal combustion. The processes running
inside the barrel of a gun are very similar to the power stroke of a 2-stroke engine where the pressurized hot combustion
gases produced by the burning fuel-air mixture push the piston downward until the exhaust port opens. In the same manner
as a car driver wants the engine to get the maximum mileage out of a given quantity of fuel, the economically-minded
shooter is interested in extracting the desired kinetic energy from the smallest possible quantity of (expensive)
powder.
One grain of black powder produces about 1.0...1.1 in3 of combustion gases (T = 273 K, p = 1013 hPa),
depending on the exact composition. These gases temporarily expand to a much greater volume because of the intense
heat released by the chemical reaction (redox reaction). If the gases are hindered from expanding, for example
by the inertia of the bullet seated in front of the powder charge, they build up a high pressure. The gas force
resulting from this pressure and the cross-sectional area of the projectile accelerates the latter and expels it
out of the barrel. After exiting the muzzle, the projectile gets decelerated by air drag.
After ignition of the powder charge, the gas pressure inside the barrel rises rapidly, passes through a maximum, and declines
asymptotically as the projectile moves forward. The acceleration of the projectile begins as soon as the gas force acting on its
base surpasses the (relatively small) static friction force. In all practical cases, the projectile leaves the barrel long before
the pressure has dropped back to atmospheric level. The pressurized gas escaping from the barrel bore at this instant produces
the muzzle blast.
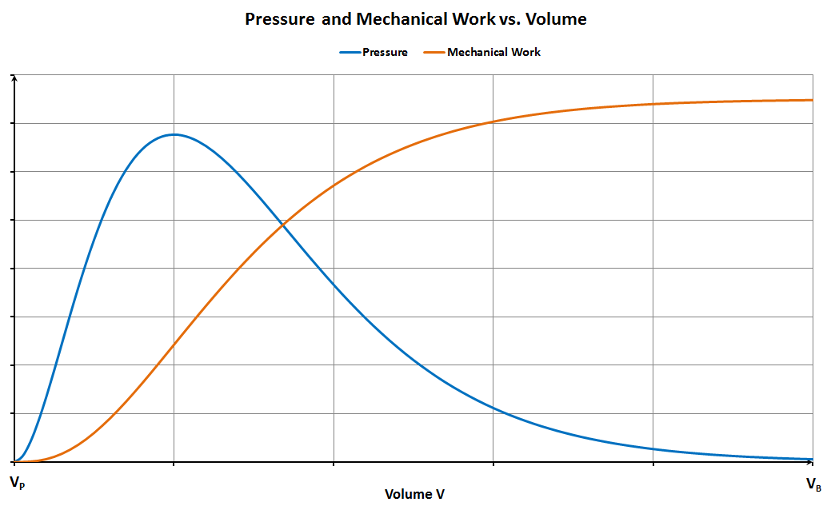
By way of example, Fig. 1 shows the gas pressure, p, inside a barrel as a function of the instantaneous volume measured between
breech plug and projectile, V (blue curve). Note that this is not the same as pressure vs. time!

|
Fig. 1 |
The orange curve in Fig. 1 indicates the mechanical work done by the expanding combustion gases, E. The latter is represented by the definite integral
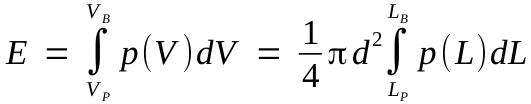
|
eq. 1 |
| E : | Total mechanical work | |
| V : | Volume measured between breech plug and base of projectile at a given instant | |
| VP : | Volume of powder charge | |
| VB : | Total bore volume | |
| d : | Bore diameter (caliber) | |
| L : | Distance measured between breech plug and base of projectile at a given instant | |
| LP : | Length of powder column | |
| LB : | Total bore length |
Geometrically, E is measured by the area between the pressure curve and the abscissa in the interval [VP,
VB].
The greater part of E remains preserved as the kinetic energy (muzzle energy) of the projectile, E0.
A certain portion of the total mechanical work is used up by the acceleration of gaseous and solid combustion products.
This is particularly the case with black powder which produces a substantial percentage of solid residues (approx. 60%) which
do not contribute to the acceleration of the projectile since they do not expand. A further, smaller portion of the mechanical
work is lost by friction.
Fig. 1 reveals that after a more or less steep rise, E asymptotically approaches a constant value as the gas pressure decreases
(ignoring friction). The same applies to E0. To reach this condition, we would need a very light powder charge or an
extremely long barrel which is not practicable.
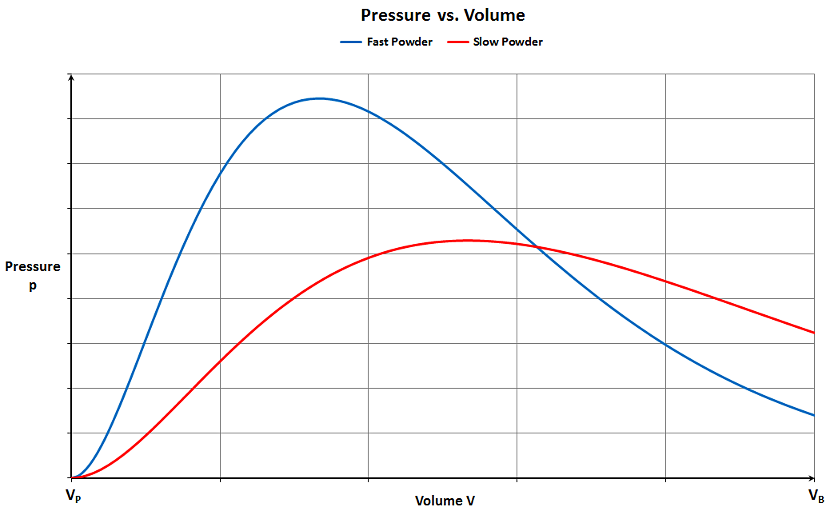
Fig. 2 displays two more realistic scenarios. With barrels of common length, there is still a considerable gas pressure
inside the bore when the ball exits the muzzle. The energy still contained in the powder gases at this instant is inevitably
lost, decreasing the energy efficiency of the process. The pressure curve for a fast-burning powder is shown in blue, the
curve for a slow-burning powder in red.
|
Fig. 2 |
Obviously, the slow powder requires a greater bore volume to achieve a sufficiently low residual pressure and, as a result, a satisfactory energy efficiency. The latter depends on several factors, among them the quotient of the total bore volume, VB, and the volume of the powder charge, VP. This quotient is called expansion ratio, R (eq. 2).
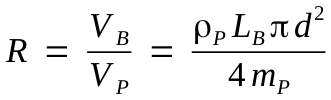
|
eq. 2 |
ρP is the bulk density (tapped) of black powder (approx. 270 grains/in3), mP
is the powder weight measured in grains.
In general, the energy efficiency of a combustion engine, η, is the quotient of the mechanical energy supplied by
the engine, E0, and the chemical energy released by the combustion of the fuel, Echem.*
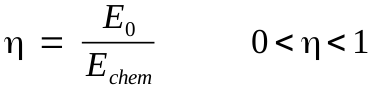
|
eq. 3 |
*It is a well-known fact that internal combustion engines with a high compression ratio (≈ expansion ratio) are more energy-efficient than engines with a low compression ratio. This is one reason why diesel-powered cars (compression ratio ≈ 16) have a better gas mileage than cars with gasoline engines (compression ratio ≈ 9).
For the shooter, it may be more convenient to define energy efficiency as the quotient of muzzle energy and powder weight:
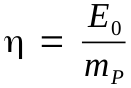
|
eq. 4 |
The curve obtained by plotting η versus R would have the same shape as the orange curve shown in Fig. 1, i. e., after a
more or less steep rise, η approaches a constant value.
Energy efficiency is mainly enhanced by:
1. High expansion ratio:
Assuming a constant powder weight, the expansion ratio rises in proportion with the bore length and the square of the bore
diameter (caliber). Thus, doubling the caliber has the same effect as quadrupling the bore length. As a result, a big-bore
pistol may be able to extract the same muzzle energy (or even more) from a given quantity of powder as a small-bore rifle.
Increasing the expansion ratio beyond a reasonable level does not lead to a further improvement of energy efficiency.
2. High burning rate of powder:
Generally, a fast-burning powder is more energy-efficient than a slow powder because it burns more completely during the
residence time of the projectile in the barrel. This results in a lower residual gas pressure at the instant the projectile
exits the muzzle. So, why should anyone want to use a slow powder at all? Because of the lower peak pressure! A heavy
charge of fast-burning powder behind a heavy long projectile might develop a peak pressure exceeding the upper limit
set by the gun manufacturer. Too high a peak pressure may further show itself by torn patches and reduced precision. While
generally 3FG powder is a good choice for handguns and small- or medium-caliber (≤ .50) rifles firing round balls, the
slower 2FG powder is better suited for rifles firing heavier long projectiles (except the smallest calibers). It is also
better for big-bore (> .50) rifles firing heavy round balls (see below). Use good judgement.
3. High projectile weight:
A suitably high projectile weight is another factor improving energy-efficiency. If we use a heavier elongated projectile
instead of a round ball, the acceleration of the projectile inside the barrel will be smaller due to its greater inert mass.
As a result, the residence time of the projectile in the barrel will increase. Thus, the red pressure curve shown in Fig. 2
will be compressed along the abscissa and assume a shape similar to the blue one. The powder will burn more completely,
resulting in a higher peak pressure and a lower residual pressure. In this way, a heavier projectile has a similar effect on
energy efficiency as a powder with a higher burning rate. Increasing the caliber works in a similar way, even with round
balls. While the gas force acting on a round ball during the shot rises with the square of the bore diameter, the inert mass
of the ball rises with the cube of the diameter. As a result, the acceleration of the ball will decrease with increasing
caliber at a given gas pressure. This, again, results in a longer residence time of the ball and a more complete burning of
the powder. Conversely, a very low projectile weight (low inertia) will prevent the build-up of a sufficiently high peak
pressure unless the powder has a very high burning rate. This is particularly observed with small-caliber round balls (see
farther below).
4. High ratio of projectile weight to powder weight:
The mechanical work done by the expanding powder gases is not only converted into the kinetic energy of the projectile but
also into the kinetic energy of the reaction products (gases and solids) of the powder itself. Thus, a high ratio of
projectile weight to powder weight improves energy efficiency because a greater portion of the total mechanical work is
available for the acceleration of the projectile. In contrast, an unreasonably heavy powder charge will not improve the
muzzle energy of the projectile to the desired extent but may result in an uncomfortable recoil of the gun.
There is another influencing factor: heat loss. The combustion gases give off heat to the cooler barrel walls. This reduces gas
temperature and pressure, and thus has a negative impact on energy efficiency. Heat exchange is promoted by a long residence
time of the projectile and by a high specific surface area of the bore (the quotient of bore surface and bore volume). The
surface area of the bore wall rises in direct proportion with the caliber while the bore volume rises with the square of the
caliber. Thus, large-caliber barrels have a lower specific surface area, a less pronounced cooling effect, and a higher thermal
efficiency.* This is partially counteracted by the longer residence time of the slower large-caliber projectiles.
*For the same reason, ship (diesel) engines with their huge cylinders have a higher thermal efficiency than the much
smaller diesel engines used in trucks and passenger cars.
The complicated interactions of expansion ratio, caliber, projectile weight, powder weight, burning rate, and heat loss make it
difficult to predict the exact muzzle energy we can extract from a given powder charge. Therefore, the average shooter mostly
has to rely on empirical data. In any event, powder weight and granulation, projectile weight, caliber, and barrel length
should be carefully adjusted to each other for best results.
The muzzle energy of a projectile is a function of its muzzle velocity, v0, and its mass, m. Thus, we can determine
E0 through velocity measurements, for example by means of a gun chronograph or a ballistic pendulum:
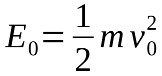
|
eq. 5* |
*I prefer calculating with metric units (kg, m/s) and convert the result to foot-pounds of energy (1 fpe = 1.3558 J).
The equation indicates that increasing energy-efficiency by raising the projectile weight may come at the cost of a
lower muzzle velocity.
Lacking the resources for extensive experiments, I did a statistical evaluation of ballistic data from the literature [1]
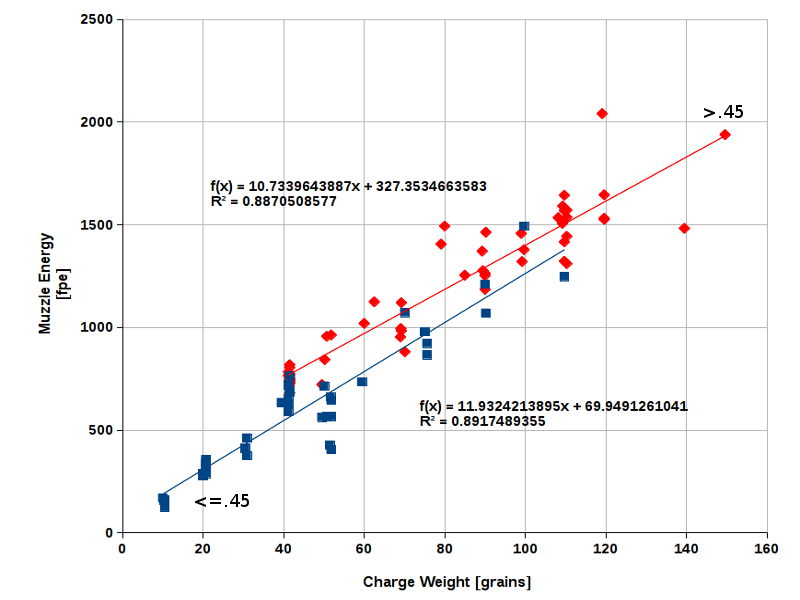
to get more insights. The results proved to be quite informative. The following scatter plot demonstrates the general
relationship between muzzle energy and powder weight (Fig. 3). The plot is based on two groups of caplock rifles of
various calibers and barrel lengths. The blue data points represent the group of small- and medium-caliber rifles
(≤ .45 cal), the red data points represent rifles with larger calibers (> .45 cal). This study includes only
ballistic data measured with round balls.
|
Fig. 3 |
What we see is a roughly (!) linear correlation between muzzle energy and powder weight. The diagram further indicates that
big-bore rifles tend to be more energy-efficient than small-bores. Due to the low coefficient of determination, a reliable
calculation of the muzzle energy resulting from a given charge weight by means of the trendline equation is not possible here.
Ignoring a few other minor factors, the muzzle energy depends on three variables: powder weight, ball weight (which is
proportional to d3 in case of round balls), and barrel length (eq. 6).
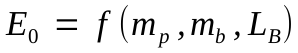
|
eq. 6 |
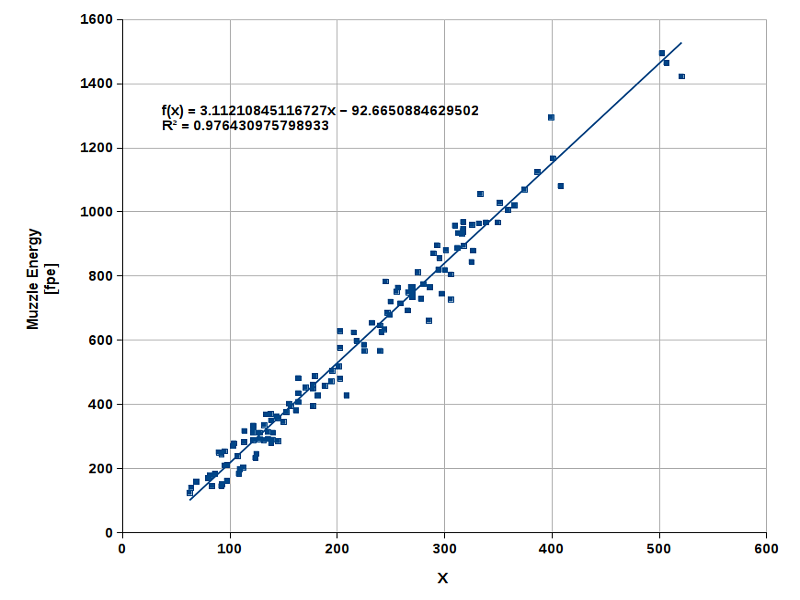
In a first, admittedly crude attempt, I plotted E0 versus the product mp ·mb ·LB but the results were not usable. Next, I tried a more refined approach and plotted E0 versus the term mpu ·mbv·LBw (denoted by X in the diagram). Now, the results look more plausible, as shown in Fig. 4.
|
Fig. 4 |
The exponents u, v, and w have been optimized so as to obtain the highest possible coefficient of determination, R2, which
was 0.976 in this case (linear regression). The optimization was done with the solver tool (nlp-solver, DEPS evolutionary algorithm)
of the spreadsheet software (LibreOffice Calc). The data set used here comprises muzzle energies of round balls (calibers ranging from
.32 to .54) fired from caplock rifles, carbines, and pistols with varying charges of 3FG powder (130 shots in total). Revolvers are not
included due to the considerable and hard-to-predict portion of gas escaping through the air gap between cylinder and barrel.
Here is the resulting trendline equation:
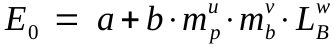
|
eq. 7 |
The constants thus found with 3FG powder are:
| a = | −92.665 |
| b = | 3.112 |
| u = | 0.738 |
| v = | 0.282 |
| w = | 0.417 |
Equation 7 yields an average value of the muzzle energy resulting from a given combination of powder weight (3FG), ball
weight (round balls only), and bore length. The equation is only valid for powder charges in the usual range and should
not be used for exotic charges, for example 100 grains of powder in combination with a .32 cal (45 grains) round ball.
Further, the equation will lead to inaccurate results when used for pocket pistols with extremely short barrels since
these are outside the observed range (LB = 6.0"- 41.5").
Example:
We have a .50 cal rifle with a bore length of 30 inches. We fire a 177-grain round ball with a charge of 60 grains of 3FG powder.
What is the approximate muzzle energy we can expect?
E0 ≈ 3.112 · 600.738 · 1770.282 · 300.417 − 92.665 ≈ 1043 fpe
As already said, this is only an estimate, and there is considerable data scattering apparent from Fig. 4 (standard error of
E0: ±49 fpe). This is not too surprising because there are other factors influencing the combustion process, as
for example powder quality, moisture content, and the seating force applied to projectile and powder charge during the loading
procedure. Further, pressure loss caused by gases escaping around the projectile (blow-by gas) contributes to data scattering.
Pressure loss is hard to predict. With round balls, it depends on ball diameter and patch thickness in relation to bore diameter
and groove depth. A patch is never a perfect gas seal but a tight-fitting ball/patch combination can reduce pressure loss to a
tolerable level. Pressure loss is further influenced by the diameter of the ignition channel. Last but not least, the combustion
process itself is random controlled to a certain degree and even under the same conditions, no powder charge burns exactly like the
other. Six shots (177 gr round ball, 70 gr 2FG powder) fired from various .50 cal rifles with the same barrel length (28")
delivered muzzle energies between approx. 880 and 1120 fpe (mean: 1010 fpe). This gives us an impression of the scattering of muzzle
energies we can expect.
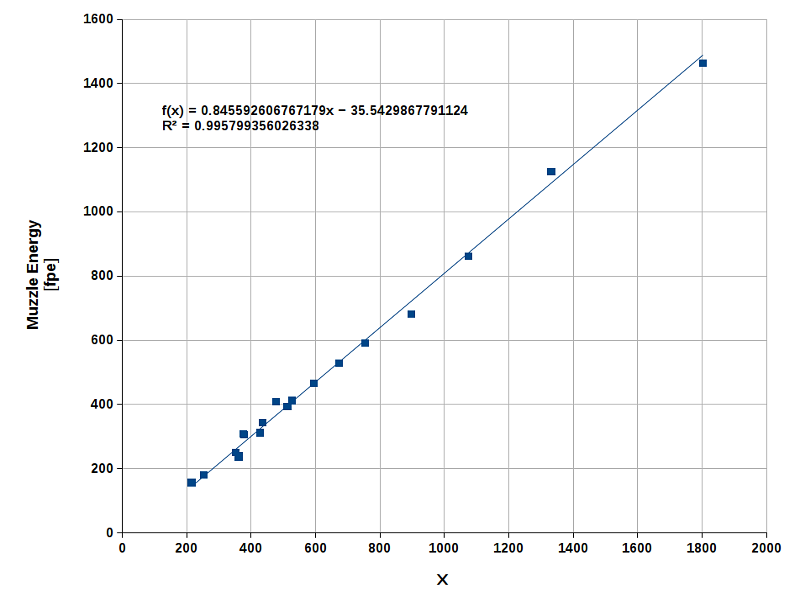
Since I was not sure about the portion of gas escaping through the vent of flintlock guns, I did a separate study comprising 20
shots (round balls, 3FG powder) fired from flintlock rifles (.32 - .50 cal) and pistols (.44 - .50 cal). After linearization, the
results within this group are surprizingly consistent (R2 = 0.996, standard error of E0 : ±24 fpe)
as shown in Fig. 5.
|
Fig. 5 |
The conspicuously small standard error may be coincidental. The constants found here are:
| a = | −35.543 |
| b = | 0.846 |
| u = | 0.824 |
| v = | 0.346 |
| w = | 0.576 |
Repeating the last calculation with the constants for flintlocks, we get:
E0 ≈ 0.846 · 600.824 · 1770.346 · 300.576 − 35.543 ≈ 1014 fpe
One might see this as an indication for an inherently greater pressure loss with flintlocks (vent). However, considering the standard
errors, the small difference between caplocks and flintlocks is not really significant here.
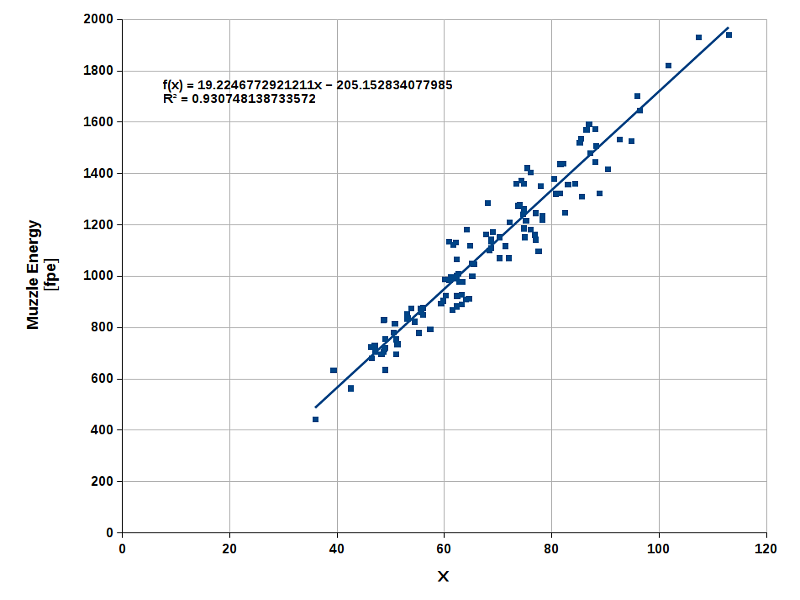
I did a similar evaluation of ballistic data obtained from 119 shots fired with the slower 2FG powder (Fig. 6). This study included
caplock rifles and carbines with calibers ranging from .36 to .54 (round balls only) but not handguns (no data available).
|
Fig. 6 |
The constants found with 2FG powder are:
| a = | -205.153 |
| b = | 19.225 |
| u = | 0.733 |
| v = | 0.146 |
| w = | 0.078 |
To my surprise, I found more data scattering here (R2 = 0.931, standard error of E0: ±79 fpe). This
may be due to the fact that the range of barrel lengths is smaller than before (no pistols). Thus, muzzle energies calculated from
this data set are less accurate.
Calculating the muzzle energy for mp = 60 gains, mb = 177 grains, and LB = 30", we now get
E0 ≈ 19.225 · 600.733 · 1770.146 · 300.078 − 205.153 ≈ 868 fpe
As we can see, 2FG powder shows a clear tendency to yield lower muzzle energies than 3FG powder (see above).
I did a similar study on ballistic data produced with rifles firing long projectiles. However, data scattering was even worse
(R2 = 0.88, standard error of E0: ±136 fpe) and the results I obtained were not really usable.
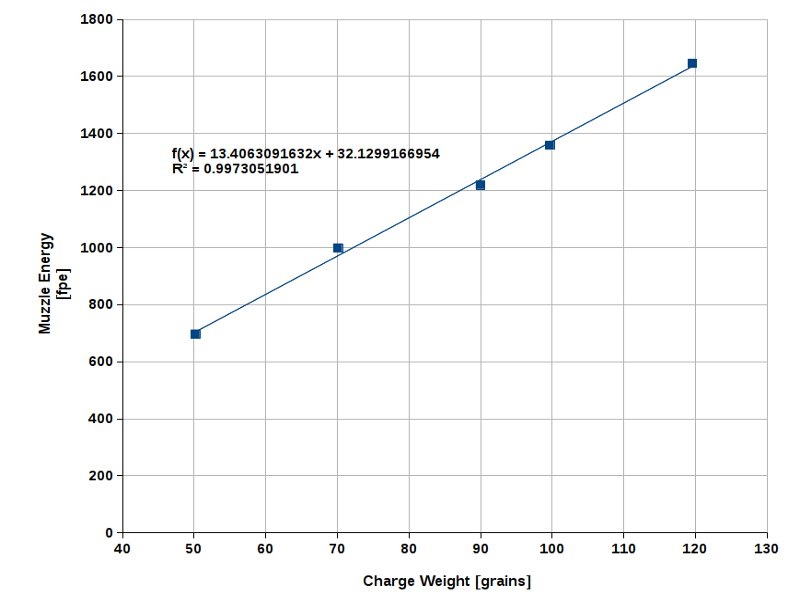
To obtain more accurate results, we have to look at a specific combination of barrel, ball, patch (if any), and powder grade. In
such a case, powder weight is the only variable while all other influencing quantities are constant. Fig. 7, for example, shows
muzzle energies observed with a .54 cal caplock rifle (32" barrel, 225 gr round ball, .01" patch, 2FG powder).
|
Fig. 7 |
Within the observed range (!), the muzzle energy is a nearly linear function of the powder weight, mp (eq. 8).
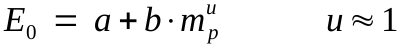
|
eq. 8 |
Again, the constants a (intercept) and b (slope) are found by linear regression. This can conveniently be done by plotting
muzzle energy versus powder weight with a spreadsheet program (scatter plot with linear trendline).
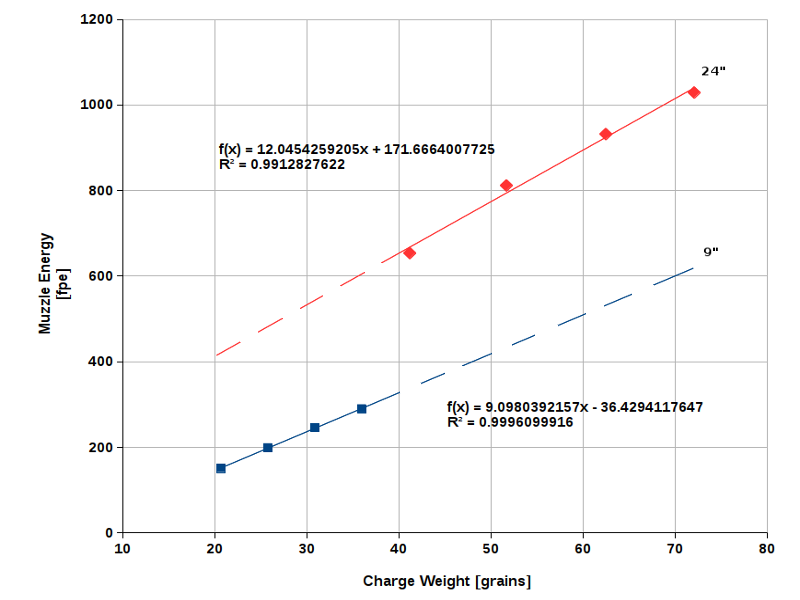
The next diagram (Fig. 8) shows a comparison between a caplock rifle (24" barrel) and a pistol (9" barrel). Both guns have
the same caliber (.45) and fire a 133 gr round ball with a .013" patch. 2FG powder was used for the rifle, the faster
3FG powder for the pistol.
|
Fig. 8 |
As expected, a long barrel is more energy-efficient than a short one. With a longer barrel we have a higher expansion ratio
and extract more energy from a given quantity of powder. Only if the residual pressure has dropped to a very low level, a
further increase of the expansion ratio will be without much effect (see Fig. 1).
If we go in the other direction and decrease the expansion ratio too much, for example by increasing the powder weight beyond
a reasonable level, the projectile will leave the barrel long before the combustion process is complete and the gas pressure has
become small enough. In such a case, energy efficiency will drop rapidly. 70 grains of powder in a .45 cal pistol barrel would
probably yield a much lower muzzle energy than suggested by linear extrapolation in Fig. 8. Thus, the linear correlation between
muzzle energy and powder weight applies only within a limited range. This is what I would call the "economical range".
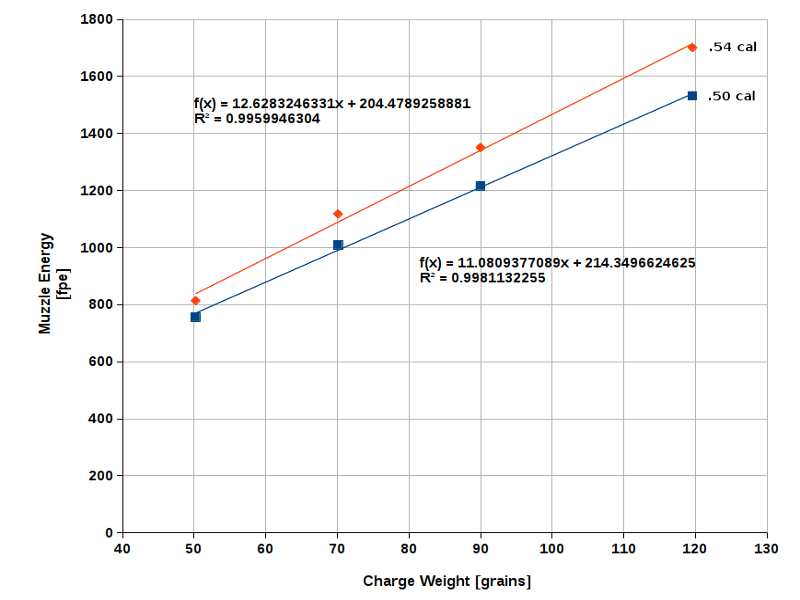
Fig. 9 demonstrates how the efficiency of the combustion process is affected by caliber and projectile weight. Here, we have
a comparison between two rifle barrels (caplock) with equal length (30" each) but different calibers: .50 cal (177 gr
round ball, 0.15" patch, 2FG powder) and .54 cal (225 gr round ball, 0.15" patch, 2FG powder), respectively.
|
Fig. 9 |
The .54 cal barrel is clearly superior to the .50 cal barrel in terms of energy efficiency. According to this diagram, the .54 cal barrel loaded with 80 grains of powder would yield about the same muzzle energy as the .50 cal barrel with 90 grains of powder. With a powder charge of 100 grains each, the .54 cal ball yields an energy of 1467 fpe (v0 = 1714 fps) while the .50 cal ball yields only 1322 fpe (v0 = 1834 fps). This confirms the tendency we have seen in Fig. 3. Why is this so? If we increase the caliber of a barrel, the bore volume will grow as well, increasing the expansion ratio and thus the energy efficiency. Doubling the cross-sectional area of a barrel bore (= multiplying the caliber by √2), for example, has the same effect as doubling the bore length. In addition, the heavier (+26%) .54 cal ball improves the efficiency of the combustion process through its greater inertia, as explained farther above.*
*These correlations may have played a role when the British began equipping many of their merchant ships and a number of naval vessels with carronades in the late 18th century although the laws of thermodynamics were not fully understood at that time. Carronades were light-weight, short-barreled cannon firing large-caliber iron balls (68-pounders were not uncommon) with comparatively small powder charges. Although they had a low muzzle velocity and a limited range, carronades had a devastating effect in close combat. Why were they so successful in their time? A possible explanation may be that they had a high expansion ratio and fired heavy projectiles, both factors ensuring that the small powder charge burnt completely and efficiently. What they lacked in muzzle velocity, they made up for in projectile weight. Moreover, the low gas pressure did not require thick-walled barrels, reducing overall weight and manufacturing costs. If used with the right tactics, these guns were able to inflict maximum damage in a most economical manner. Obviously, British merchants knew to calculate!
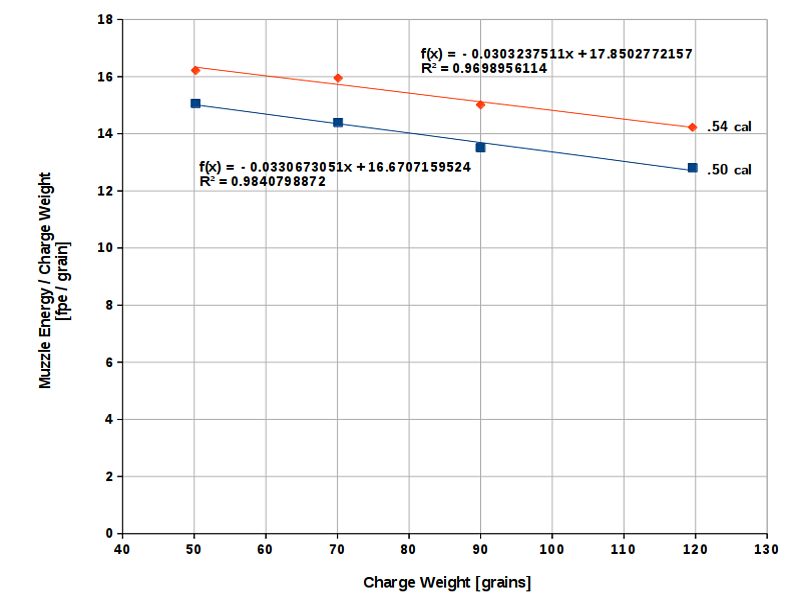
Fig. 10 shows that while the muzzle energy increases with increasing powder weight, energy efficiency, measured as the quotient of muzzle energy and powder weight, actually (slightly) decreases. This is due to the decreasing expansion ratio which results in a higher residual gas pressure (= energy loss). Moreover, if we increase the ratio of powder weight to projectile weight, a growing portion of the energy released by the powder will be used to accelerate the combustion residues of the latter. This portion is not available for the acceleration of the projectile. Last but not least, a larger quantity of powder takes more time to burn which is an additional factor increasing the residual pressure (see Fig. 2).
|
Fig. 10 |
According to Fig. 10, the .54 cal rifle barrel with a powder charge of 120 grains displays about the same energy efficiency as the
.50 cal barrel with a charge of 75 grains. In other words, in large-caliber barrels we can use much heavier charges without wasting
expensive powder! Conversely, using heavy powder charges in small caliber guns should result in poor energy efficiency, at least with
round balls.
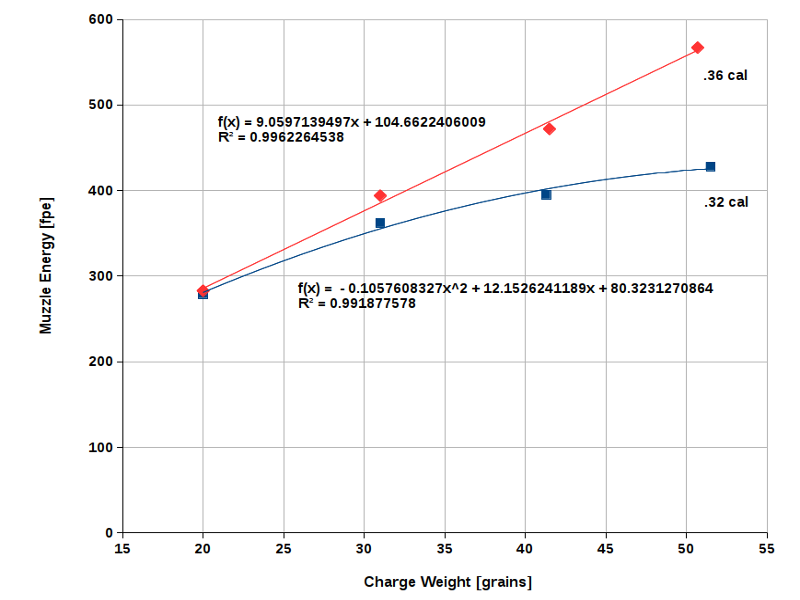
Fig. 11 shows a comparison between two small-caliber round balls (.32 cal / 45 grains and .36 cal / 65 grains) fired from caplock
rifles with similar barrel lengths (.32 cal: 26", .36 cal: 25"). Powder granulation and patch thickness are identical in
both cases (3FG, 0.013").
|
Fig. 11 |
The .36 cal ball shows the same behavior as seen in Fig. 7 through Fig. 9, i. e., a more or less linear rise of E0
with increasing powder weight. As expected, the energy gained from 50 grains of powder is smaller in this case than with big-bore
rifles (compare with Fig. 9). The real surprise is the behavior of the .32 cal ball. With a light powder charge (20 grains), it
delivers almost the same muzzle energy as the bigger .36 cal ball. However, the curve is not linear here but flattens out rapidly
as the powder weight increases (u<1). As a result, the .32 cal ball needs about 50 grains of powder to produce the same energy as a .36
cal ball with a powder charge of only 35 grains. How can we explain this? Apart from the smaller expansion ratio, the unfavorable
ratio of powder weight to ball weight probably becomes a dominant factor here. Above 45 grains, the powder weight surpasses the ball
weight in this case. This means that a high portion of the mechanical energy released by the powder is consumed to accelerate the
inert mass of the combustion products (gases and solids) and is not available to accelerate the ball. Accordingly, energy efficiency
decreases considerably. Further, the shape of the curve may also be an indication that even 3FG powder is too slow for a .32 cal
round ball. In other words, the inertia of this ball is so small that the latter gets blown out of the barrel while the combustion
process is still in full progress, possibly not far from the pressure maximum. Remember, a heavy powder charge takes more time to
burn than a light one. There must be a reason why the old .32 cal squirrel rifles sometimes had barrels as long as 40" or even
more.
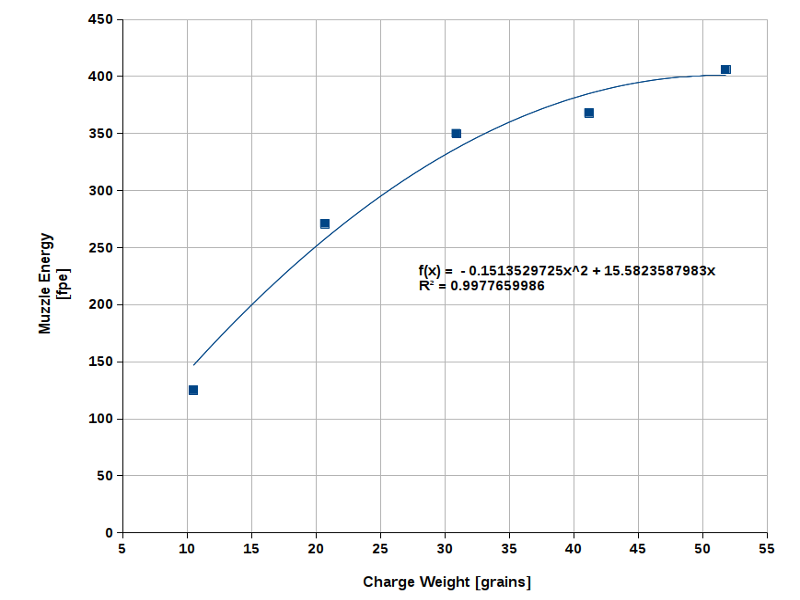
At first, I suspected the shape of the curve was an artefact caused by data scattering. However, I found a very similar curve when
looking at the ballistic data of a .32 cal ball fired from a different rifle with a 24" barrel (Fig. 12).
|
Fig. 12 |
These results suggest that using the faster 4FG powder or Swiss Powder #1 might be the better choice for .32 cal rifles when
firing round balls.
Apart from the relatively low projectile weight, there is another reason why small-caliber guns work more efficiently with a
fast-burning powder: the geometry of the powder charge. A charge of 50 grains, for example, has a length of 2.30" in a
.32 cal barrel while the length of the same charge in a .54 cal barrel is only 0.81" (assuming a bulk density of 270
grains/in3). It is easy to see that a thin, elongated powder charge needs more time to burn than a charge of a more
compact shape. Another factor slowing down combustion is the more pronounced cooling effect of the bore surface in a small-caliber
barrel (higher specific surface area). In an extremely thin bore, the powder charge would become a slow-burning fuse.
Now let us see what happens when we replace the inefficient .32 cal round ball (45 grains) with a heavier elongated projectile
of the same caliber (Maxi ball, 103 grains). Again, a rifle with a 24" barrel was used. The powder grade was 3FG, as before
(Fig. 13).
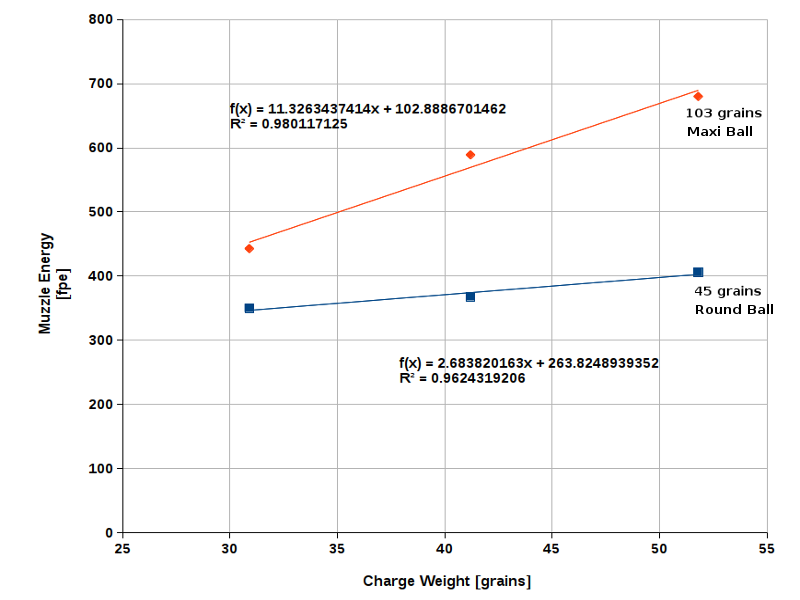
|
Fig. 13 |
As expected, the Maxi Ball delivers a much higher muzzle energy than the round ball. This is because the heavier elongated
projectile takes more time to leave the barrel due to its greater inertia which causes the powder to burn more completely.
Moreover, we have a much more favorable projectile-to-powder weight ratio here.
Even with medium-caliber round balls, a faster powder is more efficient than a slower one. By way of example, Fig. 14 shows
a comparison between 3FG and 2FG powder (.45 cal caplock rifle, 30" barrel, 133 gr round ball, .015" patch).
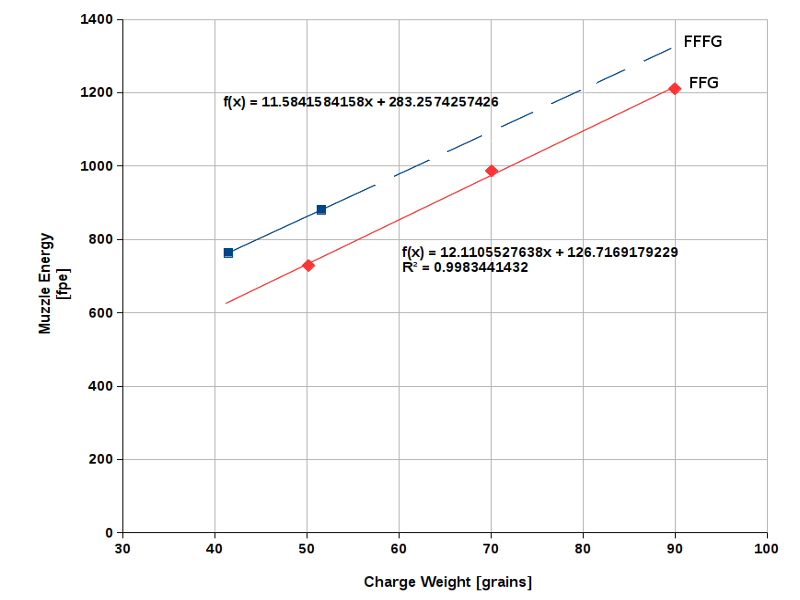
|
Fig. 14 |
It is quite surprising that in spite of the long (30") barrel, 2FG powder is relatively inefficient when compared with 3FG powder.
In this example, a 49-grain charge of 3FG powder would yield about the same muzzle energy as a 60-grain charge of 2FG
powder. A similar effect has been observed with .50 and .54 cal round balls. The only conclusion we can draw is that 3FG
powder is the more economical choice as long as we use moderate powder charges and round balls. However, we should not forget
the peak pressure! If we are using long projectiles (except small calibers), very large calibers (= heavy round balls),
or heavy powder charges, we should rather play it safe and use 2FG powder.
So, what have we learned? In terms of energy-efficiency, long barrels are better than short ones, large calibers are better
than small ones, and long projectiles are better than round balls. In general, a slow powder is good for long barrels, large
calibers, and heavy elongated projectiles while a fast powder is particularly good for small or medium calibers and round
balls. Further, a fast-burning powder and/or a heavy projectile produces a high peak pressure (which the ordinary shooter can
neither measure nor calculate).
The powder weight recommended for a given caliber, projectile type, and barrel length depends on the muzzle energy required
for the intended purpose, e. g., hunting (big game, small game) or target shooting. Knowing the desired muzzle energy, we can
solve equation 7 for the powder weight, mp, to get a first guess of the latter (eq. 9):
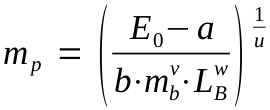
|
eq. 9 |
Remember, this is a low-precision formula obtained by statistical analysis.
Example:
We have a .54 cal rifle with a barrel length of 32 inches. The gun fires a patched round ball of 225 grains. We need
a muzzle energy of 1000 fpe. How much 2FG powder would we need approximately? With the constants for 2FG powder (see farther above),
we get:
mp ≈ [(1000 + 205.153) / (19.225 · 2250.146 · 320.078)] 1/0.733 ≈ 67 grains
How much 3FG powder would we need to obtain the same muzzle energy? We use the constants for 3FG powder and get:
mp ≈ [(1000 + 92.665) / (3.112 · 2250.282 · 320.417)] 1/0.738 ≈ 50 grains
Particularly hunters have a keen interest to know how much powder they need to achieve the required kinetic energy with their individual combination of gun, projectile, patch (if any), and powder grade. The research-minded shooter may wish to set up his own calibration curve for this purpose, as demonstrated in Fig. 7. One should start with a small powder charge and increase the latter in increments of 5 or 10 grains from shot to shot. The muzzle velocities measured with a gun chronograph have to be converted to energies (eq. 5) before plotting muzzle energy vs. powder weight with a spreadsheet program (scatter plot with trendline). It is essential to fire each shot under exactly the same conditions (except the powder weight). The first shot has to be discarded because the bore surface is not dressed with powder residues yet and may still be coated with oil. Further, a constant quantity of patch lubricant (if applicable) should be used. The time elapsed between loading the gun and firing the shot should also be fairly constant because otherwise the portion of lubricant migrating into the powder charge would vary, changing the burning rate in an uncontrollable manner (putting a layer of semolina or a felt disk on top of the powder charge may help as well). Last but not least, we have to apply the same seating force to each projectile. If these rules are observed, a fairly linear relationship between muzzle energy and powder weight should be found (similar to Fig. 7). Probably, some degree of data scattering will be observed. Obvious outliers should be discarded and the respective shot repeated. The upper limit of the economical range of powder weights is where the curve flattens out visibly (see Fig. 11). This procedure may be repeated with different powder grades, if necessary.
Addendum:
As mentioned farther above, I was not quite satisfied with the results obtained with long projectiles. Therefore, I did another statistical evaluation including round balls and long projectiles fired from various caplock rifles with 2FG powder (total number of shots: 238). Since I assumed the muzzle energy to be a function of four variables now (including the bore diameter, d), I plotted E0 versus the term d t ·mpu ·mbv·LBw (denoted by X in the diagram) this time. Fig. 15 shows the scatter plot after modifying the four exponents so as to obtain the highest possible coefficient of determination. The red data points represent round balls, the blue data points long projectiles.
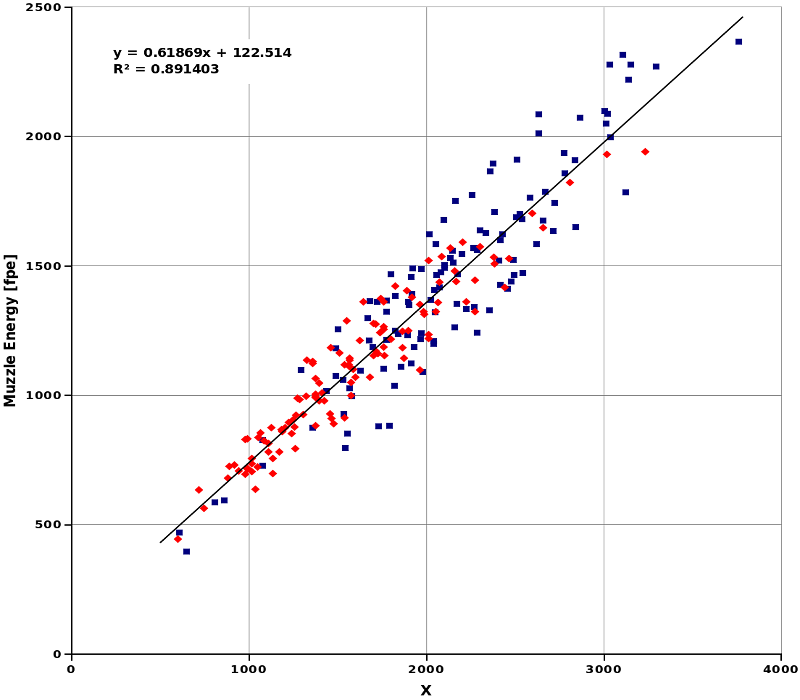
|
Fig. 15 |
In spite of the optimization, data scattering is still tremendous (R2=0.89, standard error of E0: ±129 fpe).
The optimum constants found with the solver tool of the spreadsheet software (this time I used Gnumeric) are:
| a = | 122.51 |
| b = | 0.6187 |
| t = | 8·10-16 ≈ 0 |
| u = | 0.9791 |
| v = | 0.3611 |
| w = | 0.3593 |
The most interesting result of this statistical study is that the exponent t is virtually zero, i. e., the muzzle energy is practically independent of the bore diameter (d0=1) but is almost exclusively determined by powder weight, projectile weight*, and barrel length (apart from the powder grade). Thus, we still can use equation 7 (see above) to obtain approximate muzzle energies. Statistically, a long projectile exhibits about the same muzzle energy as a round ball of the same weight (but larger caliber), provided all other parameters are kept constant.
* Of course, the weight of a projectile is a function of its caliber and shape.
Calculating the muzzle energy for mp = 60 gains, mb = 177 grains, and LB = 30" again, we now get
E0 ≈ 0.6187 · 600.9791 · 1770.3611 · 300.3593 + 122.51 ≈ 872 fpe
This result is very similar to the one obtained with round balls alone farther above (see Fig.6). However, we should expect much
greater errors when using this method to predict muzzle energies of long projectiles.
[1] Fadala, Sam. Blackpowder Loading Manual, 3rd Edition, DBI Books, Inc.; 1995: pp 169-317
This book is a must for every black-powder shooter and cannot be praised enough. The author took the trouble to fire
hundreds of test shots from a greater number of guns, measure the muzzle velocity, calculate the muzzle energy, and tabulate the
results. Further, the book contains a wealth of additional information.

